1.2 머신러닝(Machine Learning)

1.2.1 머신러닝이란?

머신러닝 : 기계나 컴퓨터가 데이터로부터 학습할 수 있도록 하는 인공지능 기술중 하나

ex) 제조업에서 공장 센서를 통해 실시간으로 데이터를 수집하여 제품의 품질을 관리하거나 이상 신호를 탐지하여 설비의 결함을 사전에 대비하는데 머신러닝을 활용한다.

인공지능 $\supset$ 머신러닝 $\supset$ 딥러닝

• 인공지능 : 머신러닝과 딥러닝을 포함한 컴퓨터과학, 전산학, 통계 개발 등 모든 관련 기술

• 머신러닝 : 정형 데이터를 활용한 인공지능 분야

• 딥러닝 : 비정형 데이터(영상, 텍스트, 음성)을 활용한 인공지능 분야

이렇게 정리하긴 했지만 이게 통용되는 것은 아니다. 그냥 머신러닝은 정형데이터에서 성능이 좋고 딥러닝은 비정형데이터에서 성능이 좋기 때문에 위처럼 통용하고 있다.

1.2.2 머신러닝 구분

• 지도학습 : 정답이 주어진 데이터를 활용하여 알고리즘을 통해 산출된 예측값과 정답을 비교하며 학습하는 방법
  • 회귀(regression), 분류(classification)

• 비지도학습 : 정답이 주어지지 않은 데이터를 탐색하여 패턴이나 내부 구조를 파악하는 학습 방법
  • 군집화(clustering), 차원 축소(dimensionality Reduction), GAN

• 강화학습 : 자신이 한 행동에 대한 보상을 받으며, 그 보상을 최대화 할수 있는 행동을 찾아내는 방법

1.2.3 지도학습(Supervised Learning)

지도학습은 정답이 있는 환경에서 입력 데이터에 대한 출력데이터를 주어 입,출력 사이 관계를 학습하는 것이다.

즉 공부한 내용과 선생님이 알려준 정답을 비교하면서 학습 능력을 키우는 과정

지도학습

• 회귀 문제 : 출력 변수가 주가, 속도, 키 ( 연속형 변수 )

• 분류 문제 : 출력 변수가 성별, 동물의 종류 (두개 혹은 그 이상의 클래스)

회귀와 분류의 차이는 바로 예측 결과와 실제 정답사이의 차이

• 회귀 : MSE
  • 예측값($\hat{y}_i$)와 실제 정답($y_i$) 사이의 차이를 의미하며 얼마나 틀렸는지를 채점하는 함수

  $$L = \frac{1}{n}\sum_{i=1}^n(y_i - \hat{y}_i)^2$$

• 분류 : CEE(Cross Entropy Error)
  • 두 확률 분포의 차이를 측정

    $$L = - \sum_{i=1}^n P(x_i)logQ(x_i)$$

• CEE 간단한 예제
  • 실제 데이터 확률분포 P, 모델이 계산한 확률분포 Q
  • 정답데이터 [0,0,1] 예측확률데이터 [0.2,0.3,0.5]
  • - (0 X log0.2 + 0 X log0.3 + 1 X log0.5) = 0.69가 손실함수이고 이를 줄여나가는 쪽으로 학습해야한다.

선형 회귀 모델

$$y = \beta_0 + \beta_1x_1 + \epsilon$$

위 식은 가장 단순한 단순 선형 회귀이다.

$\beta_0$와 $\beta_1$ 는 y절편과 기울기의 역할을 하며 회귀 계수라고 한다.

이 회귀 계수는 회귀 모델을 통해 알고 싶은 학습 Parameter(매개변수)이다.

ex) 광고비($x_1$)에 따른 제품 매출액($y)$을 알고 싶다면, 광고비와 제품 매출액의 데이터를 통해 회귀계수를 추정하는 것이다.

그렇다면 두 변수를 가장 잘 설명하는 y절편과 기울기는 어떻게 구할까?

직선을 그었을 때, 실제값과 예측값이 비슷할수록 좋은 직선식이다.

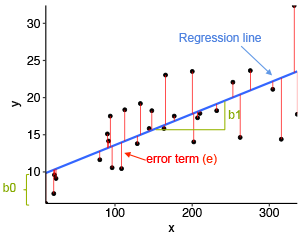
그 다음 그림에서와 마찬가지로 실제값과 예측값의 거리를 구해준다. ⇒ MSE

$$L = \frac{1}{n}\sum_{i=1}^n(y_i = \hat{y}_i)^2 = \frac{1}{n}\sum_{i=1}^n [y_i - (\hat{\beta_0} + \hat{\beta_1}x_i)]^2$$

이건 손실함수 이고 이것을 최소화 시키면서 해를 구하는 것이 바로 최소제곱법이다!

$$y = \beta_0 + \beta_1x_1 +\beta_2x_2 +.... +\epsilon$$

위 식은 다중 선형 회귀이다.

여러가지의 입력값을 이용해 예측을 하는 것이다.

하지만 이렇게 입력 변수가 많다고 좋은 것은 아니다. 이걸로 생기는 문제점을 소개하겠다.

• 과적합(Overfitting)
  • 너무 학습데이터를 과하게 학습시켜 다른 케이스에 대해서는 예측을 제대로 할 수 없는 상황

• 다중공선성(Multicollinearity)
  • 입력변수 사이에 높은 상관관계를 갖으면 두 변수가 설명하는 부분이 겹쳐서 정신을 못차리게 된다.

선형 회귀 모델의 특징

• 장점 : 설명력
  • 다른 지도학습과 비교했을 때 예측력 관점에서 우수하진 않다.
  • 출력 변수와 입력 변수 사이의 관계를 선형으로 표현해서 입력이 출력의 얼마나 영향을 끼치는지 편하게 확인 할수 있다.

1) 로지스틱 회귀 모델

출력값이 클래스처럼 범주형일 경우에 적용할 수 있는 회귀 모델 중 하나 ( 보통 2개에만 사용 3개는 복잡해서 설명력이 떨어진다)

ex) 사망 0 생존 1 로 분류 같은 예측을 할때 선형회귀를 쓸 수 없다. 이때는 로지스틱 회귀를 사용해 해결가능

이때는 Odds라는 개념을 사용

Odds : 임의의 사건이 실패할 확률 대비 성공할 확률의 비율

$$Odds = \frac{P(Y = 1)}{P(Y = 0)} = \frac{P(Y = 1)}{1 - P(Y = 1)}$$

Odds는 0부터 $\infty$의 범위를 가지므로 log를 적용해서 -$\infty$~$\infty$로 범위가 변환된다.

이렇게 되면 선형 회귀 모델을 적용할 수 있게 된다.

(오 몰랐는데! 이 Log Odds의 형태가 바로 시그모이드(sigmoid Function)이였다.... 헐.....

딥러닝을 할 때 항상 쓰던 그 함수가 ... 로그 오즈라니.. 놀랐다..)

** 2 Lasso 와 Ridg

모델링을 할 때 과적합과 다중공선성을 막기 위해 이와 같은 문제를 해결하고 일반화 된 모델을 구성하는 기법을 일반화, 여기서 Penalty Term을 추가해서 일반화를 돕는걸 정규화(Regularization)이라고 한다.

<밑에 시그마만 이해하는게 정신건강에 이롭다.>

• Lasso
  • L1-Penalty
  • $\sum|\beta_i|$

• Ridge
  • L2-Penalty
  • $\sum\beta_i^2$

  

두 방법은 손실 함수에 penalty를 추가해서 회귀 계수가 과하게 추정되는 것을 막아준다.

$$L = \sum_{i=1}^n[y_i - (\beta_0 + \sum_{j=1}^p\beta_jx_{ij})]^2 + \lambda \cdot penalty$$

위 식이 어렵다고 생각할수 있지만 그냥 다중선형회귀에 손실함수 에다가 penalty를 얼마나 가할지 람다로 조절해서 더해주는 것 뿐이다.

여기서 $\lambda$ : hyperparameter 라고 우리가 정해주는 것이다.

위 그림을 한번 보자.

이게 진짜 심오한 그림인데..

우선 위에 L을 최소화하는 회귀 계수는 저 손실함수(빨간색)과 penalty(파란색)이 맞닿는 영역이다.

Lasso 같은 경우는$\beta$의 절대값 일차식의 합이여서 저렇게 사각형이고 Ridge는 $\beta$의 제곱의 합이여서 저렇게 원형으로 모양이 나온다.

그래서 이제 결과를 보면 Lasso는 맞닿는 지점을 쭉 내려서 회귀 계수를 0으로 만들어 버렸다.

반면 Ridge는 0에 가까운 작은 수로 축소 시키는 것을 볼 수 있다.

즉 Lasso 는 전체 변수 중 일부 변수만 선택하는(중요한것만 선택 나머지 싹 버리기), Ridge는 전체적으로 0에 가까운 회귀 계수로 감소시켜 과적합과 다중공선성을 막는다.

3) 의사결정나무

입력 변수를 조합한 규칙으로 출력 변수를 예측하는 모델로 나무를 뒤집은 모양과 유사

사실 이걸 어떻게 사용하는지는 잘 모르겠다. 좀 더 공부해가면서 채우겠다.

4) Support Vector Machine(SVM)

예측성능이 높고 과적합에 면역능력이 있는 모델이다.

회귀 → SVR(Regression) , 이상치 탐지 → 1-class SVM 으로 사용한다

SVM은 클래스를 가장 잘 나눌 수 있는 결정 경계를 정하는 모델이다.

그림에서 볼 때 가운데 진한 선이 두 클래스를 분류하는 일반화 된 가장 좋은 경계선이라고 할 수 있다.

그림에서 보듯이 결정경계와 가장 가까운 포인트들을 Support Vector 라고 하고 바로 그 선을 기준으로 클래스 사이의 거리를 Margin이라고 한다.

이 margin을 최대화 하는 평면이 Hyperplane이라고 하며, 이 초평면을 찾는 것이 SVM의 목적이다.

SVM은 예측 성능이무척 좋지만 결정해야할 하이퍼파라미터들이 많고 학습 속도가 느리다는 단점이 있다.

그리고 설명하기가 힘들다는 점이 있다.

• 과적합을 방지하기 위해 어느정도 오차를 허용하는 방식을 Soft margin
  • 하이퍼 파라미터가 커질수록 마진이 줄어들어 과적합, 작을수록 마진이 커져서 과소적합이 생긴다.

• 오차를 허용하지 않는 방식을 Hard margin

K-Nearest Neighbors(K-NN)

최근접이웃접근방식이라고 해석된다.

새로운 데이터가 입력되었을 때, 가장 가까운 데이터 k개를 이용해서 해당 데이터를 유추하는 모델이다.

위 그림만 봐도 이해가 딱 될 거 같은데 A를 1,2,3,4 중 하나로 정해야 된다고 한다. 그럼 뭘로 정할 것인가?

당연히 빨강색이라고 말할것이다. 왜냐면 가까운 것들끼리 뭉쳐있는데 빨강색이 가장 가깝기 때문이다.

이 알고리즘은 직관적이고 또 높은 예측력을 갖고 있다.

하지만 새로 입력되는 데이터와 기존의 데이터 사이의 거리를 모두 계산하고 비교해야 하므로 데이터가 많을수록 학습 속도가 급격하게 느려지는 단점이 있다.

HyperParameter : k의 수

k 가 작으면 시야가 좁아지면서 과적합의 가능성이 있다.

k가 너무 크면 주변 데이터를 고려하는 의미가 사라지게 된다.

앙상블 모형

(조금 도움을 받았다. 출처 : https://bkshin.tistory.com/entry/머신러닝-11-앙상블-학습-Ensemble-Learning-배깅Bagging과-부스팅Boosting)

집단지성 : 다수의 사람이 서로 협동하거나 경쟁하면 얻는 능력 > 개인보다 뛰어남

실제로 현재 대부분의 대회에서 이 앙상블을 사용해서 좋은 성적을 거둔다고 한다.

대표적인 방법론으로 배깅, 부스팅, 랜덤 포레스트가 있다.

• 배깅 : 이미 존재하는 데이터로부터 같은 크기의 표본을 여러 번 복원추출한 부트스트랩 표본에 대해 에측 모델을 생성한 후 그 결과를 조합하는 방법론
  • 이거 이렇게 써놓으면 노양심아닌가?? 이거 첨보는 사람은 이해도 못하겠네....
  • 그냥 데이터를 여러 번 뽑아서 각 모델을 학습시키면 여러가지의 결과물이 나오는데 그 판단에 대해 투표를 해서 많이 나온쪽이 정답이라고 판단해버리는 시스템이다
  • 예를들어, 데이터를 6 집합으로 쪼개서 각각 학습을 돌린다음 4개가 A라고 2개가 B라고 하면 다수결로 A라고 판단해 버리는 것이다.

• 부스팅 : 가중치를 활용하여 약 분류기를 강 분류기로 만드는 방법이다.
  • Decision Tree 1 과 Decision Tree2가 서로 독립적으로 결과를 예측한다.
  • 그 다음 그 결과를 집계해서 최종 결과 값을 예측하는 시스템인데
  • 처음 모델이 예측을 하면 거기에 가중치가 부여되고 이것을 다음 모델에 영향을 준다.
  • 잘못 분류된 데이터에 집중해서 새로운 분류 규칙을 만드는데 반복한다.

  

  • D1에서는 세 가지의 오분류가 일어났다. 잘못 분류된 데이터의 가중치를 높여줬다.
  • 그 결과 D2에서 잘 분류된건 크기를 줄였고 잘못 분류한건 키웠다.
  • D3에서도 이를 반복하면서 최종적으로 잘 분류 된것을 확인할 수 있다.

• 랜덤포레스트 : 배깅의 일종으로 의사결정 나무가 모여 숲을 이룬 것 같은 형태로 나무 모델링 단계에서 변수를 랜덤으로 선택하여 진행하는 방법론
  • 그냥 배깅에서 좀 더 발전한건데 50개의 feature가 있다고 가정하자
  • 그 중 5개 만 뽑아서 결정 트리를 만들고 또 랜덤으로 5개 뽑아서 결정트리 만들어서
  • 이렇게 숲을 만든다음 투표해서 결과를 예측하는 것이다.

Uploaded by Notion2Tistory v1.1.0