딥러닝의 성능을 높여주는 핵심 알고리즘에 대해서 설명하겠다.
미니배치(Mini Batch)
딥러닝의 경우 머신러닝에 비해 대용량의 데이터가 필요하다.
데이터가 무척 크고 복잡한 계산을 함으로써 메모리 한계에 부딪히기도 하고 딥러닝을 돌리는데 아주 좋은 컴퓨터를 쓰는 ai 연구 팀도 돌리는데 하루가 걸린다고 한다.
그래서! 작은 단위로 나누어서 학습한다. 앞에서 설명했던 학습, 검증, 테스트 데이터로 나누는 것과는 다르다.
- 미니 배치1 / 미니배치 2/ 미니배치3 / 미니배치 4 ...
- 일단 미니 배치만큼 경사하강법이나 역전파 알고리즘을 써서 다음 미니 배치로 넘어간다
- 이렇게 모든 배치를 돌면 1epoch가 끝났다고 한다.
ex) 데이터가 2000개 이고 배치 크기를 200으로 하자
- 그럼 Iteration(파라미터 업데이트 횟수) 는 10이다.
경사하강법(Gradient Descent)
적용 사례
선형 회귀 모델에서는 보통 MSE를 사용한다.
- 식에 따르면 포물선의 형태로 나타나는데 최적의 회귀계수는 손실함수가 가장 작은 부분이다.
- MSE를 회귀계수로 미분해서 기울기가 0이 되는 지점이 바로 그곳이다.
- ML파트에서 자세히 설명했으므로 이렇게만 짚고 가겠다.
신경망에서는 Feed Forward, Back Propagation 을 반복하면서 최적의 가중치를 탐색한다.
- 이에 대한 설명도 앞에 고생하면서 작성했으므로 넘어가겠다.
경사하강법 원리
원리 : 눈을 가리고 지도나 나침반 없이 산속에서 가장 낮은 지점으로 내려가는 것,
즉 산에 혼자 서 있다면 기울기가 아래로 가파른 곳으로 우리는 내려갈 것이다. 그렇게 반복하다보면 땅 끝으로 도달 할 수 있다.
결론적으로 경사하강법은 현재 손실 함수의 위치에서 가장 기울기가 가파른 방향으로 학습 Parameter를 업데이트 하는 것이다. 이 과정에서 미분이 사용된다.
학습률
이제 산에서 어느 방향으로 내려갈 지 정했다면 얼마나 내려갈지, 보폭을 정해야 한다.
바로 이것이 학습률이다. 너무 크거나 작으면 문제가 생기는건 당연해 보인다.

그림으로 보면 어떻게 학습률을 잡아야 할지 고민할 수 있다.
공식
https://mathtbro.tistory.com/76
부족하지만 대충 optimizer 함수(sgd, momentum, adagrad, rmsprop, Adam) 을 정리했다.
활성 함수
인공신경망이 좋은 이유 중 하나 → 비선형 활성 함수를 사용하기 때문이다.
why? → 선형 함수를 사용하게 되면 기울기에 곱만 되는 형식으로 여러개의 은닉층을 거쳐도 결국은 하나의 은닉층을 쓴 성능을 보인다.
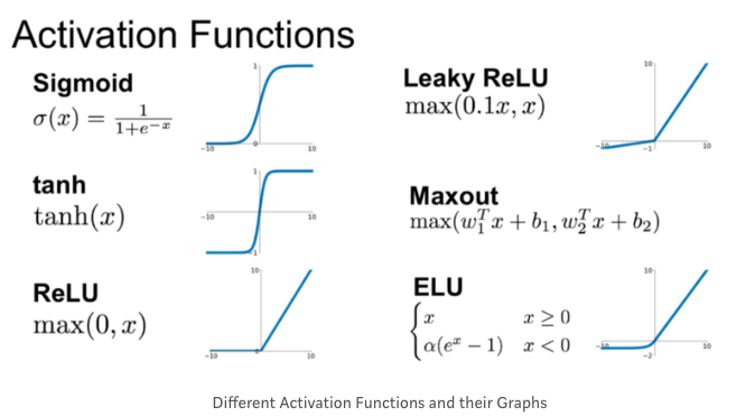
시그모이드를 가장 많이 사용했지만 시그모이드는 0또는 1에 가까우면 기울기가 0에 아주 가까운 값이 되서 업데이트를 할 때 별 효가가 없어서 가중치 학습이 잘 되지않는 Gradient Vanishing이 일어난다.
이를 극복하기 위해 미분가능한 ReLU, ELU같은 다양한 함수를 쓰는 여기가 지속되고 있다.
출력 함수
회귀문제 : identity function
분류문제 : softmax
Uploaded by Notion2Tistory v1.1.0